Specular reflection: Difference between revisions
en>Srleffler Nonsense. Absorption of light does not imply a violation of conservation of energy. Energy is not "absorbed", but light is. |
No edit summary |
||
| Line 1: | Line 1: | ||
In [[mathematics]], '''nonlinear programming''' ('''NLP''') is the process of solving an [[optimization problem]] defined by a [[Simultaneous equations|system]] of [[equation|equalities]] and [[inequalities]], collectively termed [[Constraint (mathematics)|constraints]], over a set of unknown [[real variable]]s, along with an objective [[function (mathematics)|function]] to be maximized or minimized, where some of the constraints or the objective function are [[nonlinear]].<ref>{{cite book | |||
| last = Bertsekas | |||
| first = Dimitri P. | |||
| authorlink = Dimitri P. Bertsekas | |||
| title = Nonlinear Programming | |||
| edition = Second | |||
| publisher = Athena Scientific | |||
| year = 1999 | |||
| location = Cambridge, MA. | |||
| isbn = 1-886529-00-0 | |||
}}</ref> It is the sub-field of [[Mathematical optimization]] that deals with problems that are not linear. | |||
==Applicability== | |||
A typical non[[Convex_optimization|convex]] problem is that of optimising transportation costs by selection from a set of transportion methods, one or more of which exhibit [[Economy of scale|economies of scale]], with various connectivities and capacity constraints. An example would be petroleum product transport given a selection or combination of pipeline, rail tanker, road tanker, river barge, or coastal tankship. Owing to economic batch size the cost functions may have discontinuities in addition to smooth changes. | |||
Modern engineering practice involves much numerical optimization. Except in certain narrow but important cases such as passive electronic circuits, engineering problems are non-linear, and they are usually very complicated. | |||
In experimental science, some simple data analysis (such as fitting a spectrum with a sum of peaks of known location and shape but unknown magnitude) can be done with linear methods, but in general these problems, also, are non-linear. Typically, one has a theoretical model of the system under study with variable parameters in it and a model the experiment or experiments, which may also have unknown parameters. One tries to find a best fit numerically. In this case one often wants a measure of the precision of the result, as well as the best fit itself. | |||
== The general non-linear optimization problem (NLP) == | |||
The problem can be stated simply as: | |||
:<math>\max_{x \in X}f(x)</math> to maximize some variable such as product throughput | |||
or | |||
:<math>\min_{x \in X}f(x)</math> to minimize a cost function | |||
where | |||
:<math>f: R^n \to R</math> | |||
:<math>x \in R^n</math> | |||
s.t. (subject to) | |||
:<math>h_i(x)=0, i \in I={1,\dots,p}</math> | |||
:<math>g_j(x) \leq 0, j \in J={1,\dots,m}</math> | |||
== Possible solutions == | |||
* feasible, that is, for an optimal solution <math>x</math> subject to constraints, the objective function <math>f</math> is either maximized or minimized. | |||
* unbounded, that is, for some <math>x</math> subject to constraints, the objective function <math>f</math> is either <math>\infty</math> or <math>-\infty</math>. | |||
* infeasible, that is, there is no solution <math>x</math> that is subject to constraints. | |||
==Methods for solving the problem== | |||
If the objective function ''f'' is linear and the constrained [[Euclidean space|space]] is a [[polytope]], the problem is a [[linear programming]] problem, which may be solved using well known linear programming solutions. | |||
If the objective function is [[Concave function|concave]] (maximization problem), or [[Convex function|convex]] (minimization problem) and the constraint set is [[Convex set|convex]], then the program is called convex and general methods from [[convex optimization]] can be used in most cases. | |||
If the objective function is a ratio of a concave and a convex function (in the maximization case) and the constraints are convex, then the problem can be transformed to a convex optimization problem using [[fractional programming]] techniques. | |||
Several methods are available for solving nonconvex problems. One approach is to use special formulations of linear programming problems. Another method involves the use of [[branch and bound]] techniques, where the program is divided into subclasses to be solved with convex (minimization problem) or linear approximations that form a lower bound on the overall cost within the subdivision. With subsequent divisions, at some point an actual solution will be obtained whose cost is equal to the best lower bound obtained for any of the approximate solutions. This solution is optimal, although possibly not unique. The algorithm may also be stopped early, with the assurance that the best possible solution is within a tolerance from the best point found; such points are called ε-optimal. Terminating to ε-optimal points is typically necessary to ensure finite termination. This is especially useful for large, difficult problems and problems with uncertain costs or values where the uncertainty can be estimated with an appropriate reliability estimation. | |||
Under [[differentiability]] and [[constraint qualification]]s, the [[Karush–Kuhn–Tucker conditions|Karush–Kuhn–Tucker (KKT) conditions]] provide necessary conditions for a solution to be optimal. Under convexity, these conditions are also sufficient. If some of the functions are non-differentiable, [[subderivative|subdifferential]] versions of | |||
[[Karush–Kuhn–Tucker conditions|Karush–Kuhn–Tucker (KKT) conditions]] are available.<ref> | |||
{{cite book|last=[[Andrzej Piotr Ruszczyński|Ruszczyński]]|first=Andrzej|title=Nonlinear Optimization|publisher=[[Princeton University Press]]|location=Princeton, NJ|year=2006|pages=xii+454|isbn=978-0691119151 |mr=2199043}}</ref> | |||
==Examples== | |||
===2-dimensional example=== | |||
[[Image:Nonlinear programming.svg|200px|thumb|right|The intersection of the line with the constrained space represents the solution]] | |||
A simple problem can be defined by the constraints | |||
:''x''<sub>1</sub> ≥ 0 | |||
:''x''<sub>2</sub> ≥ 0 | |||
:''x''<sub>1</sub><sup>2</sup> + ''x''<sub>2</sub><sup>2</sup> ≥ 1 | |||
:''x''<sub>1</sub><sup>2</sup> + ''x''<sub>2</sub><sup>2</sup> ≤ 2 | |||
with an objective function to be maximized | |||
:''f''('''x''') = ''x''<sub>1</sub> + ''x''<sub>2</sub> | |||
where '''x''' = (''x''<sub>1</sub>, ''x''<sub>2</sub>). [http://apmonitor.com/online/view_pass.php?f=2d.apm Solve 2-D Problem]. | |||
===3-dimensional example=== | |||
[[Image:Nonlinear programming 3D.svg|thumb|right|The intersection of the top surface with the constrained space in the center represents the solution]] | |||
Another simple problem can be defined by the constraints | |||
:''x''<sub>1</sub><sup>2</sup> − ''x''<sub>2</sub><sup>2</sup> + ''x''<sub>3</sub><sup>2</sup> ≤ 2 | |||
:''x''<sub>1</sub><sup>2</sup> + ''x''<sub>2</sub><sup>2</sup> + ''x''<sub>3</sub><sup>2</sup> ≤ 10 | |||
with an objective function to be maximized | |||
:''f''('''x''') = ''x''<sub>1</sub>''x''<sub>2</sub> + ''x''<sub>2</sub>''x''<sub>3</sub> | |||
where '''x''' = (''x''<sub>1</sub>, ''x''<sub>2</sub>, ''x''<sub>3</sub>). [http://apmonitor.com/online/view_pass.php?f=3d.apm Solve 3-D Problem]. | |||
==See also== | |||
* [[Curve fitting]] | |||
* [[Least squares]] minimization | |||
* [[Linear programming]] | |||
* [[nl (format)]] | |||
* [[Mathematical optimization]] | |||
* [[List of optimization software]] | |||
*[[Werner Fenchel]] | |||
==References== | |||
<references/> | |||
==Further reading== | |||
* Avriel, Mordecai (2003). ''Nonlinear Programming: Analysis and Methods.'' Dover Publishing. ISBN 0-486-43227-0. | |||
* Bazaraa, Mokhtar S. and Shetty, C. M. (1979). ''Nonlinear programming. Theory and algorithms.'' John Wiley & Sons. ISBN 0-471-78610-1. | |||
* Bertsekas, Dimitri P. (1999). ''Nonlinear Programming: 2nd Edition.'' Athena Scientific. ISBN 1-886529-00-0. | |||
* {{cite book|last1=Bonnans|first1=J. Frédéric|last2=Gilbert|first2=J. Charles|last3=Lemaréchal|first3=Claude| authorlink3=Claude Lemaréchal|last4=Sagastizábal|first4=Claudia A.|title=Numerical optimization: Theoretical and practical aspects|url=http://www.springer.com/mathematics/applications/book/978-3-540-35445-1|edition=Second revised ed. of translation of 1997 <!-- ''Optimisation numérique: Aspects théoriques et pratiques'' --> French| series=Universitext|publisher=Springer-Verlag|location=Berlin|year=2006|pages=xiv+490|isbn=3-540-35445-X|doi=10.1007/978-3-540-35447-5|mr=2265882}} | |||
* {{cite book|last1=Luenberger|first1=David G.|authorlink1=David G. Luenberger|last2=Ye|first2=Yinyu|authorlink2=Yinyu Ye|title=Linear and nonlinear programming|edition=Third|series=International Series in Operations Research & Management Science|volume=116|publisher=Springer|location=New York|year=2008|pages=xiv+546|isbn=978-0-387-74502-2 | mr = 2423726}} | |||
* Nocedal, Jorge and Wright, Stephen J. (1999). ''Numerical Optimization.'' Springer. ISBN 0-387-98793-2. | |||
* [[Jan Brinkhuis]] and Vladimir Tikhomirov, 'Optimization: Insights and Applications', 2005, Princeton University Press | |||
==External links== | |||
*[http://neos-guide.org/non-lp-faq Nonlinear programming FAQ] | |||
*[http://glossary.computing.society.informs.org/ Mathematical Programming Glossary] | |||
*[http://www.lionhrtpub.com/orms/surveys/nlp/nlp.html Nonlinear Programming Survey OR/MS Today] | |||
*[http://apmonitor.com/wiki/index.php/Main/Background Overview of Optimization in Industry] | |||
{{optimization algorithms}} | |||
{{DEFAULTSORT:Nonlinear Programming}} | |||
[[Category:Mathematical optimization]] | |||
[[Category:Optimization algorithms and methods]] | |||
Revision as of 18:32, 27 November 2013
In mathematics, nonlinear programming (NLP) is the process of solving an optimization problem defined by a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are nonlinear.[1] It is the sub-field of Mathematical optimization that deals with problems that are not linear.
Applicability
A typical nonconvex problem is that of optimising transportation costs by selection from a set of transportion methods, one or more of which exhibit economies of scale, with various connectivities and capacity constraints. An example would be petroleum product transport given a selection or combination of pipeline, rail tanker, road tanker, river barge, or coastal tankship. Owing to economic batch size the cost functions may have discontinuities in addition to smooth changes.
Modern engineering practice involves much numerical optimization. Except in certain narrow but important cases such as passive electronic circuits, engineering problems are non-linear, and they are usually very complicated.
In experimental science, some simple data analysis (such as fitting a spectrum with a sum of peaks of known location and shape but unknown magnitude) can be done with linear methods, but in general these problems, also, are non-linear. Typically, one has a theoretical model of the system under study with variable parameters in it and a model the experiment or experiments, which may also have unknown parameters. One tries to find a best fit numerically. In this case one often wants a measure of the precision of the result, as well as the best fit itself.
The general non-linear optimization problem (NLP)
The problem can be stated simply as:
or
where
s.t. (subject to)
Possible solutions
- feasible, that is, for an optimal solution subject to constraints, the objective function is either maximized or minimized.
- unbounded, that is, for some subject to constraints, the objective function is either or .
- infeasible, that is, there is no solution that is subject to constraints.
Methods for solving the problem
If the objective function f is linear and the constrained space is a polytope, the problem is a linear programming problem, which may be solved using well known linear programming solutions.
If the objective function is concave (maximization problem), or convex (minimization problem) and the constraint set is convex, then the program is called convex and general methods from convex optimization can be used in most cases.
If the objective function is a ratio of a concave and a convex function (in the maximization case) and the constraints are convex, then the problem can be transformed to a convex optimization problem using fractional programming techniques.
Several methods are available for solving nonconvex problems. One approach is to use special formulations of linear programming problems. Another method involves the use of branch and bound techniques, where the program is divided into subclasses to be solved with convex (minimization problem) or linear approximations that form a lower bound on the overall cost within the subdivision. With subsequent divisions, at some point an actual solution will be obtained whose cost is equal to the best lower bound obtained for any of the approximate solutions. This solution is optimal, although possibly not unique. The algorithm may also be stopped early, with the assurance that the best possible solution is within a tolerance from the best point found; such points are called ε-optimal. Terminating to ε-optimal points is typically necessary to ensure finite termination. This is especially useful for large, difficult problems and problems with uncertain costs or values where the uncertainty can be estimated with an appropriate reliability estimation.
Under differentiability and constraint qualifications, the Karush–Kuhn–Tucker (KKT) conditions provide necessary conditions for a solution to be optimal. Under convexity, these conditions are also sufficient. If some of the functions are non-differentiable, subdifferential versions of Karush–Kuhn–Tucker (KKT) conditions are available.[2]
Examples
2-dimensional example
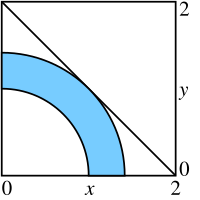
A simple problem can be defined by the constraints
- x1 ≥ 0
- x2 ≥ 0
- x12 + x22 ≥ 1
- x12 + x22 ≤ 2
with an objective function to be maximized
- f(x) = x1 + x2
where x = (x1, x2). Solve 2-D Problem.
3-dimensional example

Another simple problem can be defined by the constraints
- x12 − x22 + x32 ≤ 2
- x12 + x22 + x32 ≤ 10
with an objective function to be maximized
- f(x) = x1x2 + x2x3
where x = (x1, x2, x3). Solve 3-D Problem.
See also
- Curve fitting
- Least squares minimization
- Linear programming
- nl (format)
- Mathematical optimization
- List of optimization software
- Werner Fenchel
References
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑
20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
Further reading
- Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
- Bazaraa, Mokhtar S. and Shetty, C. M. (1979). Nonlinear programming. Theory and algorithms. John Wiley & Sons. ISBN 0-471-78610-1.
- Bertsekas, Dimitri P. (1999). Nonlinear Programming: 2nd Edition. Athena Scientific. ISBN 1-886529-00-0.
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - Nocedal, Jorge and Wright, Stephen J. (1999). Numerical Optimization. Springer. ISBN 0-387-98793-2.
- Jan Brinkhuis and Vladimir Tikhomirov, 'Optimization: Insights and Applications', 2005, Princeton University Press









