Doping (semiconductor)

The barometric formula, sometimes called the exponential atmosphere or isothermal atmosphere, is a formula used to model how the pressure (or density) of the air changes with altitude.

Pressure equations

DTZ's public sale group in Singapore auctions all forms of residential, workplace and retail properties, outlets, homes, lodges, boarding homes, industrial buildings and development websites. Auctions are at present held as soon as a month.

We will not only get you a property at a rock-backside price but also in an space that you've got longed for. You simply must chill out back after giving us the accountability. We will assure you 100% satisfaction. Since we now have been working in the Singapore actual property market for a very long time, we know the place you may get the best property at the right price. You will also be extremely benefited by choosing us, as we may even let you know about the precise time to invest in the Singapore actual property market.

The Hexacube is offering new ec launch singapore business property for sale Singapore investors want to contemplate. Residents of the realm will likely appreciate that they'll customize the business area that they wish to purchase as properly. This venture represents one of the crucial expansive buildings offered in Singapore up to now. Many investors will possible want to try how they will customise the property that they do determine to buy by means of here. This location has offered folks the prospect that they should understand extra about how this course of can work as well.

Singapore has been beckoning to traders ever since the value of properties in Singapore started sky rocketing just a few years again. Many businesses have their places of work in Singapore and prefer to own their own workplace area within the country once they decide to have a everlasting office. Rentals in Singapore in the corporate sector can make sense for some time until a business has discovered a agency footing. Finding Commercial Property Singapore takes a variety of time and effort but might be very rewarding in the long term.

is changing into a rising pattern among Singaporeans as the standard of living is increasing over time and more Singaporeans have abundance of capital to invest on properties. Investing in the personal properties in Singapore I would like to applaud you for arising with such a book which covers the secrets and techniques and tips of among the profitable Singapore property buyers. I believe many novice investors will profit quite a bit from studying and making use of some of the tips shared by the gurus." – Woo Chee Hoe Special bonus for consumers of Secrets of Singapore Property Gurus Actually, I can't consider one other resource on the market that teaches you all the points above about Singapore property at such a low value. Can you? Condominium For Sale (D09) – Yong An Park For Lease

In 12 months 2013, c ommercial retails, shoebox residences and mass market properties continued to be the celebrities of the property market. Models are snapped up in report time and at document breaking prices. Builders are having fun with overwhelming demand and patrons need more. We feel that these segments of the property market are booming is a repercussion of the property cooling measures no.6 and no. 7. With additional buyer's stamp responsibility imposed on residential properties, buyers change their focus to commercial and industrial properties. I imagine every property purchasers need their property funding to understand in value.

Pressure as a function of the height above the sea level

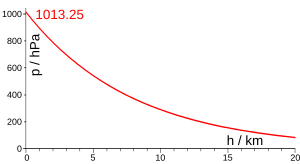
There are two different equations for computing pressure at various height regimes below 86 km (or 278,400 feet). The first equation is used when the value of Standard Temperature Lapse Rate is not equal to zero; the second equation is used when standard temperature lapse rate equals zero.

Equation 1:

${P}=P_{b}\cdot \left[{\frac {T_{b}}{T_{b}+L_{b}\cdot (h-h_{b})}}\right]^{\textstyle {\frac {g_{0}\cdot M}{R^{*}\cdot L_{b}}}}$

Equation 2:

$P=P_{b}\cdot \exp \left[{\frac {-g_{0}\cdot M\cdot (h-h_{b})}{R^{*}\cdot T_{b}}}\right]$

where

$P_{b}$ = Static pressure (pascals)

$T_{b}$ = Standard temperature (K)

$L_{b}$ = Standard temperature lapse rate -0.0065 (K/m) in ISA

$h$ = Height above sea level (meters)

$h_{b}$ = Height at bottom of layer b (meters; e.g., $h_{1}$ = 11,000 meters)

$R^{*}$ = Universal gas constant for air: 8.31432 N·m /(mol·K)

$g_{0}$ = Gravitational acceleration (9.80665 m/s²)

$M$ = Molar mass of Earth's air (0.0289644 kg/mol)

Or converted to Imperial units:

where

$P_{b}$ = Static pressure (inches of mercury, inHg)

$T_{b}$ = Standard temperature (K)

$L_{b}$ = Standard temperature lapse rate (K/ft)

$h$ = Height above sea level (ft)

$h_{b}$ = Height at bottom of layer b (feet; e.g., $h_{1}$ = 36,089 ft)

$R^{*}$ = Universal gas constant; using feet, kelvins, and (SI) moles: 8.9494596×10⁴ lb·ft²/(lbmol·K·s²)

$g_{0}$ = Gravitational acceleration (32.17405 ft/s²)

$M$ = Molar mass of Earth's air (28.9644 lb/lbmol)

The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. In these equations, g₀, M and R^* are each single-valued constants, while P, L, T, and h are multivalued constants in accordance with the table below. The values used for M, g₀, and $R^{*}$ are in accordance with the U.S. Standard Atmosphere, 1976, and the value for $R^{*}$ in particular does not agree with standard values for this constant. The reference value for P_b for b = 0 is the defined sea level value, P₀ = 101325 pascals or 29.92126 inHg. Values of P_b of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when $h=h_{b+1}$.:

Subscript b	Height above sea level		Static pressure		Standard temperature (K)	Temperature lapse rate
	(m)	(ft)	(pascals)	(inHg)		(K/m)	(K/ft)
0	0	0	101325.00	29.92126	288.15	-0.0065	-0.0019812
1	11,000	36,089	22632.10	6.683245	216.65	0.0	0.0
2	20,000	65,617	5474.89	1.616734	216.65	0.001	0.0003048
3	32,000	104,987	868.02	0.2563258	228.65	0.0028	0.00085344
4	47,000	154,199	110.91	0.0327506	270.65	0.0	0.0
5	51,000	167,323	66.94	0.01976704	270.65	-0.0028	-0.00085344
6	71,000	232,940	3.96	0.00116833	214.65	-0.002	-0.0006096

Density equations

The expressions for calculating density are nearly identical to calculating pressure. The only difference is the exponent in Equation 1.

There are two different equations for computing density at various height regimes below 86 geometric km (84,852 geopotential meters or 278,385.8 geopotential feet). The first equation is used when the value of Standard Temperature Lapse rate is not equal to zero; the second equation is used when Standard Temperature Lapse rate equals zero.

Equation 1:

${\rho }=\rho _{b}\cdot \left[{\frac {T_{b}+L_{b}\cdot (h-h_{b})}{T_{b}}}\right]^{\left(-{\frac {g_{0}\cdot M}{R^{*}\cdot L_{b}}}\right)-1}$

Equation 2:

${\rho }=\rho _{b}\cdot \exp \left[{\frac {-g_{0}\cdot M\cdot (h-h_{b})}{R^{*}\cdot T_{b}}}\right]$

where

${\rho }$ = Mass density (kg/m³)

$T$ = Standard temperature (K)

$L$ = Standard temperature lapse rate (see table below) (K/m) in ISA

$h$ = Height above sea level (geopotential meters)

$R^{*}$ = Universal gas constant for air: 8.31432 N·m/(mol·K)

$g_{0}$ = Gravitational acceleration (9.80665 m/s²)

$M$ = Molar mass of Earth's air (0.0289644 kg/mol)

Or converted to English gravitational foot-pound-second units:

Where

${\rho }$ = Mass density (slug/ft³)

${T}$ = Standard temperature (kelvins)

${L}$ = Standard temperature lapse rate (degrees Celsius per foot)

${h}$ = Height above sea level (geopotential feet)

${R^{*}}$ = Universal gas constant (8.9494596×10⁴ ft²/(s·°C))

${g_{0}}$ = Gravitational acceleration (32.17405 ft/s²)

${M}$ = Molar mass of Earth's air (0.0289644 kg/mol)

The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. The reference value for $\rho _{b}$ for b = 0 is the defined sea level value, $\rho _{o}$ = 1.2250 kg/m³ or 0.0023768908 slug/ft³. Values of $\rho _{b}$ of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when $h=h_{b+1}$

In these equations, g₀, M and R^* are each single-valued constants, while $\rho$, L, T and h are multi-valued constants in accordance with the table below. The values used for M, g₀ and R^* are in accordance with the U.S. Standard Atmosphere, 1976, and that the value for R^* in particular does not agree with standard values for this constant.

Subscript b	Height Above Sea Level (h)		Mass Density ($\rho$)		Standard Temperature (T') (K)	Temperature Lapse Rate (L)
	(m)	(ft)	(kg/m3)	(slugs/ft3)		(K/m)	(K/ft)
0	0	0	1.2250	2.3768908 x 10−3	288.15	-0.0065	-0.0019812
1	11,000	36,089.24	0.36391	7.0611703 x 10−4	216.65	0.0	0.0
2	20,000	65,616.79	0.08803	1.7081572 x 10−4	216.65	0.001	0.0003048
3	32,000	104,986.87	0.01322	2.5660735 x 10−5	228.65	0.0028	0.00085344
4	47,000	154,199.48	0.00143	2.7698702 x 10−6	270.65	0.0	0.0
5	51,000	167,322.83	0.00086	1.6717895 x 10−6	270.65	-0.0028	-0.00085344
6	71,000	232,939.63	0.000064	1.2458989 x 10−7	214.65	-0.002	-0.0006096

Derivation

The barometric formula can be derived fairly easily using the ideal gas law:

$\rho ={\frac {M\cdot P}{R^{*}\cdot T}}$

When density is known:

$P={\frac {\rho \cdot {R^{*}}\cdot T}{M}}$

And assuming that all pressure is hydrostatic:

$dP=-\rho g\,dz\,$

Dividing the $dP$ by the $P$ expression we get:

${\frac {dP}{P}}=-{\frac {Mg\,dz}{R^{*}T}}$

Integrating this expression from the surface to the altitude z we get:

$P=P_{0}e^{-\int _{0}^{z}{Mgdz/R^{*}T}}\,$

Assuming constant temperature, molar mass, and gravitational acceleration, we get the barometric formula:

$P=P_{0}e^{-Mgz/R^{*}T}\,$

In this formulation, $R^{*}$ is the gas constant, and the term $R^{*}T/Mg$ gives the scale height (approximately equal to 8.4 km for the troposphere).

(For exact results, it should be remembered that atmospheres containing water do not behave as an ideal gas. See real gas or perfect gas or gas for further understanding)

Estimating the temperature

Assuming that the only energy source is from the sun, and the albedo is constant throughout the planet, we can get an estimate of a constant temperature. The solar energy flux at a distance $R_{\mathrm {AU} }$ can be estimated as:

$f_{\odot }={\frac {L_{\odot }}{4\pi R_{\mathrm {AU} }^{2}}},$

where $L_{\odot }$ is the solar luminosity. The actual incoming energy can be estimated as

$E_{in}=f_{\odot }(1-\alpha )\pi R_{\oplus }^{2}$

where $\alpha$ is the albedo of the planet. $R_{\oplus }$ is the radius of the planet and $R_{\mathrm {AU} }$ is the distance to the Sun in astronomical units. The outgoing energy can be estimated using the Stefan-Boltzmann's law

$E_{out}=4\pi R_{\oplus }^{2}\sigma T_{eq}^{4}$

where $\sigma$ is the Stefan–Boltzmann constant and $T_{eq}$ is the temperature at equilibrium. Solving the equation:

$E_{in}=E_{out}\,$

leads to the following estimate of a planet's temperature

$T_{eq}={\sqrt[{4}]{\frac {L_{\odot }(1-\alpha )}{16\pi \sigma R_{\mathrm {AU} }^{2}}}}$

which for Earth is about 255 K or −18 °C

See also

• NRLMSISE-00