Main Page: Difference between revisions
Karl3982vrl (talk | contribs) mNo edit summary |
Karl3982vrl (talk | contribs) mNo edit summary |
||
| Line 1: | Line 1: | ||
{{quantum mechanics}} | |||
In [[quantum mechanics]], the '''angular momentum operator''' is one of several related [[operator (mathematics)|operators]] analogous to classical [[angular momentum]]. The angular momentum operator plays a central role in the theory of [[atomic physics]] and other quantum problems involving [[rotational symmetry]]. In both classical and quantum mechanical systems, angular momentum (together with linear momentum and energy) is one of the three fundamental properties of motion.<ref name="Liboff">Introductory Quantum Mechanics, [[Richard L. Liboff]], 2nd Edition, ISBN 0-201-54715-5</ref> | |||
There are several angular momentum operators: '''total angular momentum''' (usually denoted '''J'''), '''orbital angular momentum''' (usually denoted '''L'''), and '''spin angular momentum''' ('''spin''' for short, usually denoted '''S'''). The term "angular momentum operator" can (confusingly) refer to either the total or the orbital angular momentum. Total angular momentum is always [[conservation of angular momentum|conserved]], see [[Noether's theorem]]. | |||
==Spin, orbital, and total angular momentum== | |||
| | {{main|Spin (physics)}} | ||
[[File:LS coupling.svg|250px|thumb|"Vector cones" of total angular momentum '''J''' (purple), orbital '''L''' (blue), and spin '''S''' (green). The cones arise due to [[quantum uncertainty]] between measuring angular momentum components ([[#Visual interpretation|see below]]).]] | |||
| | |||
The [[angular momentum|classical definition of angular momentum]] is <math>\mathbf{L}=\mathbf{r}\times\mathbf{p}</math>. This can be carried over to quantum mechanics, by reinterpreting '''r''' as the quantum [[position operator]] and '''p''' as the quantum [[momentum operator]]. '''L''' is then an [[Operator (physics)|operator]], specifically called the ''orbital angular momentum operator''. Specifically, '''L''' is a ''vector operator'', meaning <math>\mathbf{L}=(L_x,L_y,L_z)</math>, where ''L''<sub>x</sub>, ''L''<sub>y</sub>, ''L''<sub>z</sub> are three different operators. | |||
However, there is another type of angular momentum, called [[spin (physics)|''spin angular momentum'']] (more often shortened to ''spin''), represented by the spin operator '''S'''. Almost all [[elementary particle]]s have spin. Spin is often depicted as a particle literally spinning around an axis, but this is a misleading and inaccurate picture: Spin is an intrinsic property of a particle, unrelated to any sort of motion in space. All [[elementary particles]] have a characteristic spin, for example [[electron]]s always have "spin 1/2" while [[photon]]s always have "spin 1". | |||
Finally, there is [[total angular momentum]] '''J''', which combines both the spin and orbital angular momentum of a particle or system: | |||
:<math>\mathbf{J}=\mathbf{L}+\mathbf{S}.</math> | |||
[[Conservation of angular momentum]] states that '''J''' for a closed system, or '''J''' for the whole universe, is conserved. However, '''L''' and '''S''' are ''not'' generally conserved. For example, the [[spin–orbit interaction]] allows angular momentum to transfer back and forth between '''L''' and '''S''', with the total '''J''' remaining constant. | |||
==Orbital angular momentum operator== | |||
Orbital angular momentum '''L''' is mathematically defined as the [[cross product]] of a wave function's [[position operator]] ('''r''') and [[momentum operator]] ('''p'''): | |||
<math> | :<math>\mathbf{L}=\mathbf{r}\times\mathbf{p}</math> | ||
This is analogous to the definition of [[angular momentum]] in classical physics. | |||
In the special case of a single particle with no [[electric charge]] and no [[spin (physics)|spin]], the angular momentum operator can be written in the position basis as a single vector equation: | |||
:<math>\mathbf{L}=-i\hbar(\mathbf{r}\times\nabla)</math> | |||
where ∇ is the vector differential operator, [[del]]. | |||
==Commutation relations== | |||
===Commutation relations between components=== | |||
The orbital angular momentum operator is a vector operator, meaning it can be written in terms of its vector components <math>\mathbf{L}=(L_x,L_y,L_z)</math>. The components have the following [[commutation relation]]s with each other:<ref>{{cite book|url=http://books.google.com/books?id=dRsvmTFpB3wC&pg=PA171|title= Quantum Mechanics|first=G. |last=Aruldhas|page=171|chapter= formula (8.8)|isbn=978-81-203-1962-2|date=2004-02-01}}</ref> | |||
:<math>[L_x,L_y]=i\hbar L_z, \;\; [L_y,L_z]=i\hbar L_x, \;\; [L_z,L_x]=i\hbar L_y</math> | |||
or in symbols, | |||
:<math>[L_l, L_m ] = i \hbar \varepsilon_{lmn} L_n</math>, | |||
where ''ε<sub>lmn</sub>'' denotes the [[Levi-Civita symbol]], and ''l,m,n'' are Cartesian coordinates (each can be ''x'', ''y'' or ''z''), and [, ] is the [[commutator]] | |||
:<math>[X,Y] \equiv XY-YX</math>. | |||
These can be proved as a direct consequence of the [[canonical commutation relation]]s <math>[x_l,p_m]=i \hbar \delta_{lm}</math>, where ''δ<sub>lm</sub>'' is the [[Kronecker delta]]. | |||
There is an analogous relationship to the commutator in classical physics which is central to the theory of canonical transformations of [[Hamilton's equations]] of motion:<ref>H. Goldstein, C. P. Poole and J. Safko, ''Classical Mechanics, 3rd Edition'', Addison-Wesley 2002, pp. 388 ff.</ref> | |||
:<math>[u, v]_{q,p} = \frac{\partial u}{\partial q_i} \frac{\partial v}{\partial p_i} - \frac{\partial u}{\partial p_i} \frac{\partial v}{\partial q_i}\!</math> | |||
(summation over generalized coordinate index i implied) where, in this bilinear expression, <math>[u, v]_{q,p}</math> is the [[Poisson bracket]] of two functions <math>u, v</math> with respect to the canonical (generalized) coordinates <math>(p,q)</math>. "... identification of the canonical angular momentum as the generator of rigid rotation of [a system of particles] leads to a number of interesting and important Poisson bracket relations."<ref>Idem, pp. 408-411.</ref> Among these are: | |||
:<math>[L_l, L_m ] = \varepsilon_{lmn} L_n. \!</math> | |||
Here, <math>L_z</math>, for example, is a transformation generated by the generalized momentum conjugate to <math>q_i</math>: | |||
:<math>L_z(q, p) = p_i</math>. | |||
It can be shown<ref>Idem, p. 404.</ref> (using Cartesian coordinates x, y and z for each particle i in the system) that | |||
:<math>L_z = x_ip_{iy} - y_ip_{ix}</math>. | |||
This generating function <math>L_z</math> has the physical significance of being the ''z''-component of the total angular momentum: | |||
:<math>L_z \ \equiv \ (r_i \ \times \ p_i)_z</math>. | |||
It is important to recognize that the Poisson bracket is an analogue, not the commutator in disguise. Hamilton's equations do not generalize to quantum mechanics because they assume that the position and momentum of a particle can be known simultaneously to infinite precision at any point in time. See the section "Generalization to quantum mechanics through Poisson bracket" in the article on [[Hamiltonian mechanics]] for details and additional references. | |||
<math> | The same commutation relations apply for the other angular momentum operators (spin and total angular momentum):<ref name=littlejohn/> | ||
:<math>[S_l, S_m ] = i \hbar \sum_{n=1}^{3} \varepsilon_{lmn} S_n, \quad [J_l, J_m ] = i \hbar \sum_{n=1}^{3} \varepsilon_{lmn} J_n</math>. | |||
These can be ''assumed'' to hold in analogy with '''L'''. Alternatively, they can be ''derived'' as discussed [[#Connection to commutation relations|below]]. | |||
These commutation relations mean that '''L''' has the mathematical structure of a [[Lie algebra]]. In this case, the Lie algebra is [[SU(2)]] or [[SO(3)]], the rotation group in three dimensions. The same is true of '''J''' and '''S'''. The reason is discussed [[#Total angular momentum as a generator of rotations|below]]. | |||
These commutation relations are relevant for measurement and uncertainty, as discussed further below. | |||
== | ===Commutation relations involving vector magnitude=== | ||
Like any vector, a [[Euclidean norm|magnitude]] can be defined for the orbital angular momentum operator, | |||
:<math>L^2 \equiv L_x^2 + L_y^2 + L_z^2</math> . | |||
'''''L'''''<sup>2</sup> is another quantum [[operator (mathematics)|operator]]. It commutes with the components of '''''L''''', | |||
:<math>[L^2,L_x] = [L^2,L_y] = [L^2,L_z] = 0~.\,</math> | |||
One way to prove that these operators commute is to start from the [''L''<sub>ℓ</sub>, ''L''<sub>''m''</sub>] commutation relations in the previous section: | |||
:{| class="toccolours collapsible collapsed" width="80%" style="text-align:left" | |||
!Click [show] on the right to see a proof of [''L''<sup>2</sup>, ''L''<sub>x</sub>] = 0, starting from the [''L''<sub>ℓ</sub>, ''L''<sub>''m''</sub>] commutation relations<ref>{{cite book | author=Griffiths, David J. | title=Introduction to Quantum Mechanics | publisher=[[Prentice Hall]] | year=1995 | page=146}}</ref> | |||
|- | |||
|<math>[L^2, L_x] = (L_x^2 + L_y^2 + L_z^2)L_x - L_x (L_x^2 + L_y^2 + L_z^2) </math> | |||
:::<math> = L_y(L_y L_x - L_x L_y) + (L_y L_x - L_x L_y) L_y + L_z(L_z L_x - L_x L_z) + (L_z L_x - L_x L_z)L_z </math> | |||
:::<math> = L_y [L_y, L_x] + [L_y, L_x] L_y + L_z [L_z, L_x] + [L_z, L_x] L_z </math> | |||
:::<math> = L_y (-i \hbar L_z) + (-i \hbar L_z) L_y + L_z (i \hbar L_y) + (i \hbar L_y) L_z </math> | |||
:::<math> = 0 </math> | |||
|} | |||
< | Mathematically, '''''L'''''<sup>2</sup> is a [[Casimir invariant]] of the [[Lie algebra]] SO(3) spanned by '''''L'''''. | ||
< | |||
In the classical case, '''''L''''' is the orbital angular momentum of the entire system of particles, '''''n''''' is the unit vector along one of the Cartesian axes and we also have Poisson pseudo-commutation of '''''L''''' with each of its Cartesian components:<ref>Goldstein et al, p. 410</ref> | |||
:<math>[\mathbf L \cdot \mathbf L, \mathbf L \cdot \mathbf n] = [L^2, \mathbf L \cdot \mathbf n] = 0</math> | |||
with <math> \mathbf n </math> selecting one of the Cartesian components of <math> \mathbf L </math>. | |||
The same commutation relations apply for the other angular momentum operators (spin and total angular momentum): | |||
:<math>[S^2,S_i]=0, \quad [J^2,J_i]=0</math> . | |||
===Uncertainty principle=== | |||
{{main|Uncertainty principle|Uncertainty principle derivations}} | |||
In general, in quantum mechanics, when two [[observable|observable operators]] do not commute, they are called ''incompatible observables''. Two incompatible observables cannot be measured simultaneously; instead they satisfy an [[uncertainty principle]]. The more accurately one observable is known, the less accurately the other one can be known. Just as there is an uncertainty principle relating position and momentum, there are uncertainty principles for angular momentum. | |||
The [[uncertainty principle|Robertson–Schrödinger relation]] gives the following uncertainty principle: | |||
:<math>\sigma_{L_x} \sigma_{L_y} \geq \frac{\hbar}{2} \left| \langle L_z \rangle \right|.</math> | |||
where <math>\sigma_X</math> is the [[standard deviation]] in the measured values of ''X'' and <math>\langle X \rangle</math> denotes the [[Expectation value (quantum mechanics)|expectation value]] of ''X''. This inequality is also true if ''x,y,z'' are rearranged, or if ''L'' is replaced by ''J'' or ''S''. | |||
Therefore, two orthogonal components of angular momentum cannot be simultaneously known or measured, except in special cases such as <math>L_x=L_y=L_z=0</math>. | |||
< | |||
It is, however, possible to simultaneously measure or specify ''L''<sup>2</sup> and any one component of ''L''; for example, ''L''<sup>2</sup> and ''L''<sub>z</sub>. This is often useful, and the values are characterized by [[azimuthal quantum number]] and [[magnetic quantum number]], as discussed further below. | |||
=== | ==Quantization== | ||
{{see also|Azimuthal quantum number|Magnetic quantum number}} | |||
In [[quantum mechanics]], angular momentum is ''quantized'' – that is, it cannot vary continuously, but only in "quantum leaps" between certain allowed values. For any system, the following restrictions on measurement results apply, where <math>\hbar</math> is [[reduced Planck constant]]: | |||
{| class="wikitable" | |||
|- | |||
!If you [[measurement in quantum mechanics|measure]]... | |||
!...the result can be... | |||
!Notes | |||
|- | |||
|''L''<sub>z</sub> | |||
|<math>(\hbar m)</math>, where <math>m\in\{\ldots, -2, -1, 0, 1, 2, \ldots\}</math> | |||
|''m'' is sometimes called "[[magnetic quantum number]]".<br />This same quantization rule holds for any component of '''L''', e.g. ''L''<sub>x</sub> or ''L''<sub>y</sub>.<br /> This rule is sometimes called '''spatial quantization'''.<ref>I''ntroduction to quantum mechanics: with applications to chemistry'', by Linus Pauling, Edgar Bright Wilson, page 45, [http://books.google.com/books?id=D48aGQTkfLgC&pg=PA45&dq=spatial+quantization google books link]</ref> | |||
|- | |||
|''S''<sub>z</sub> or ''J''<sub>z</sub> | |||
|<math>(\hbar m)</math>, where <math>m\in\{\ldots, -1, -0.5, 0, 0.5, 1, 1.5, \ldots\}</math> | |||
|For ''S''<sub>z</sub>, ''m'' is sometimes called "[[spin quantum number|spin projection quantum number]]".<br /> For ''J''<sub>z</sub>, ''m'' is sometimes called "[[Azimuthal quantum number#Total angular momentum of an electron in the atom|total angular momentum projection quantum number]]".<br />This same quantization rule holds for any component of '''S''' or '''J''', e.g. ''S''<sub>x</sub> or ''J''<sub>y</sub>. | |||
|- | |||
|<math>L^2</math> | |||
|<math>(\hbar^2 \ell (\ell+1))</math>, where <math>\ell \in \{0,1,2,\ldots\}</math> | |||
|''L''<sup>2</sup> is defined by <math>L^2 \equiv L_x^2 +L_y^2 + L_z^2</math>.<br /><math>\ell</math> is sometimes called "[[azimuthal quantum number]]" or "orbital quantum number". | |||
|- | |||
|<math>S^2</math> | |||
|<math>(\hbar^2 s(s+1))</math>, where <math>s \in \{ 0,0.5,1,1.5, \ldots \}</math> | |||
|''s'' is called [[spin quantum number]] or just "spin". For example, a [[spin-½|spin-½ particle]] is a particle where ''s''=½. | |||
|- | |||
|<math>J^2</math> | |||
|<math>(\hbar^2 j(j+1))</math>, where <math>j \in \{ 0,0.5,1,1.5, \ldots \} </math> | |||
|''j'' is sometimes called "[[Azimuthal quantum number#Total angular momentum of an electron in the atom|total angular momentum quantum number]]". | |||
|- | |||
|<math>L^2</math> and <math>L_z</math><br />simultaneously | |||
|<math>(\hbar^2 \ell(\ell+1))</math> for <math>L^2</math>, and <math>(\hbar m_\ell)</math> for <math>L_z</math><br />where <math>\ell \in \{ 0,1,2,\ldots \}</math> and <br /><math>m_\ell \in \{ -\ell, (-\ell+1), \ldots, (\ell-1),\ell \}</math> | |||
|(See above for terminology.) | |||
|- | |||
|<math>S^2</math> and <math>S_z</math><br />simultaneously | |||
|<math>(\hbar^2 s(s+1))</math> for <math>S^2</math>, and <math>(\hbar m_s)</math> for <math>S_z</math><br />where <math>s \in \{0,0.5,1,1.5,\ldots\}</math> and<br /><math>m_s \in \{ -s, (-s+1), \ldots, (s-1),s\}</math> | |||
|(See above for terminology.) | |||
|- | |||
|<math>J^2</math> and <math>J_z</math><br />simultaneously | |||
|<math>(\hbar^2 j(j+1))</math> for <math>J^2</math>, and <math>(\hbar m_j)</math> for <math>J_z</math><br />where <math>j \in \{ 0,0.5,1,1.5,\ldots \}</math> and <br /><math>m_j \in \{ -j, (-j+1), \ldots, (j-1),j \}</math> | |||
|(See above for terminology.) | |||
|} | |||
[[File:Circular Standing Wave.gif|thumb|right|In this [[standing wave]] on a circular string, the circle is broken into exactly 8 [[wavelength]]s. A standing wave like this can have 0,1,2, or any integer number of wavelengths around the circle, but it ''cannot'' have a non-integer number of wavelengths like 8.3. In quantum mechanics, angular momentum is quantized for a similar reason.]] | |||
===Derivation using ladder operators=== | |||
{{main|Ladder operator#Angular momentum}} | |||
A common way to derive the quantization rules above is the method of ''[[ladder operator]]s''.<ref name=Griffithsladder>{{cite book | author=Griffiths, David J. | title=Introduction to Quantum Mechanics | publisher=[[Prentice Hall]] | year=1995 | pages=147–149}}</ref> The ladder operators are defined: | |||
:<math>J_+ \equiv J_x + i J_y, \quad J_- \equiv J_x - i J_y</math> | |||
Suppose a state <math>| \psi \rangle</math> is a state in the simultaneous eigenbasis of <math>J^2</math> and <math>J_z</math> (i.e., a state with a single, definite value of <math>J^2</math> and a single, definite value of <math>J_z</math>). Then using the commutation relations, one can prove that <math>J_+|\psi\rangle</math> and <math>J_-|\psi\rangle</math> are ''also'' in the simultaneous eigenbasis, with the same value of <math>J^2</math>, but where <math>J_z |\psi\rangle</math> is increased or decreased by <math>\hbar</math>, respectively. (It is also possible that one or both of these vectors is the zero vector.) (For a proof, see [[ladder operator#angular momentum]].) | |||
By manipulating these ladder operators and using the commutation rules, it is possible to prove almost all of the quantization rules above. | |||
{| class="toccolours collapsible collapsed" width="75%" style="text-align:left" | |||
!Click [show] on the right to see more details in the ladder-operator proof of the quantization rules<ref name=Griffithsladder/> | |||
|- | |||
|Before starting the main proof, we will note a useful fact: That <math>J_x^2,J_y^2,J_z^2</math> are [[positive-semidefinite matrix|positive-semidefinite operator]]s, meaning that all their eigenvalues are nonnegative. That also implies that the same is true for their sums, including <math>J^2 = J_x^2 + J_y^2 + J_z^2</math> and <math>(J^2 - J_z^2) = (J_x^2 + J_y^2)</math>. The reason is because the square of ''any'' [[Hermitian operator]] is always positive semidefinite. (A Hermitian operator has real eigenvalues, so the squares of those eigenvalues are nonnegative.) | |||
As above, assume that a state <math>| \psi \rangle</math> is a state in the simultaneous eigenbasis of <math>J^2</math> and <math>J_z</math>. Its eigenvalue with respect to <math>J^2</math> can be written in the form <math>\hbar^2 j (j+1)</math> for some real number ''j'' > 0 (because as mentioned in the previous paragraph, <math>J^2</math> has nonnegative eigenvalues), and its eigenvalue with respect to <math>J_z</math> can be written <math>\hbar m</math> for some real number ''m''. Instead of <math>| \psi \rangle</math> we will use the more descriptive notation <math>|\psi \rangle = | j,m \rangle</math>. | |||
Next, consider the sequence ("ladder") of states | |||
:<math>\{\ldots \; , \; J_- J_- | j,m \rangle \; , \; J_- | j,m \rangle \; , \; | j,m \rangle \; , \; J_+ | j,m \rangle \; , \; J_+ J_+ | j,m \rangle \; , \; \ldots \} </math> | |||
Some entries in this infinite sequence may be the [[zero vector]] (as we will see). However, as described above, all the nonzero entries have the same value of <math>J^2</math>, and among the nonzero entries, each entry has a value of <math>J_z</math> which is exactly <math>\hbar</math> more than the previous entry. | |||
<math> | In this ladder, there can only be a finite number of nonzero entries, with infinite copies of the zero vector on the left and right. The reason is, as mentioned above, <math>(J^2 - J_z^2)</math> is positive-semidefinite, so if any quantum state is an eigenvector of both <math>J^2</math> and <math>J_z^2</math>, the former eigenvalue is larger. The states in the ladder all have the same <math>J^2</math> eigenvalue, but going very far to the left or the right, the <math>J_z^2</math> eigenvalue gets larger and larger. The only possible resolution is, as mentioned, that there are only finitely many nonzero entries in the ladder. | ||
< | |||
Now, consider the last nonzero entry to the right of the ladder, <math>|j,m_{max} \rangle</math>. This state has the property that <math>J_+ |j,m_{max}\rangle = 0</math>. As proven in the [[ladder operator]] article, | |||
:<math>J_+ |j,m \rangle = \hbar \sqrt{j(j+1) - m(m+1)}|j,m+1\rangle</math> | |||
If this is zero, then <math>j(j+1) = m_{max}(m_{max}+1)</math>, so <math>j=m</math> or <math>j = -m - 1</math>. However, because <math>J^2 - J_z^2</math> is positive-semidefinite, <math>\hbar^2 j(j+1) \geq (\hbar m)^2</math>, which means that the only possibility is <math>m_{max} = j</math>. | |||
Similarly, consider the first nonzero entry on the left of the ladder, <math>|j, m_{min}\rangle</math>. This state has the property that | |||
<math>J_- |j,m_{min}\rangle = 0</math>. As proven in the [[ladder operator]] article, | |||
:<math>J_- |j,m\rangle = \hbar \sqrt{j(j+1) - m(m-1)} |j,m-1\rangle</math> | |||
As above, the only possibility is that <math>m_{min} = -j</math> | |||
Since ''m'' changes by 1 on each step of the ladder, <math>(j - (-j))</math> is an integer, so ''j'' is an integer or half-integer (0 or 0.5 or 1 or 1.5...). | |||
|} | |||
Since '''S''' and '''L''' have the same commutation relations as '''J''', the same ladder analysis works for them. | |||
The ladder-operator analysis does '''''not''''' explain one aspect of the quantization rules above: the fact that '''L''' (unlike '''J''' and '''S''') cannot have half-integer quantum numbers. This fact can be proven (at least in the special case of one particle) by writing down every possible eigenfunction of ''L''<sup>2</sup> and ''L''<sub>z</sub>, (they are the [[spherical harmonic]]s), and seeing explicitly that none of them have half-integer quantum numbers.<ref>{{cite book | author=Griffiths, David J. | title=Introduction to Quantum Mechanics | publisher=[[Prentice Hall]] | year=1995 | pages=148–153}}</ref> An alternative derivation is [[#SU(2), SO(3), and 360° rotations|below]]. | |||
===Visual interpretation=== | |||
[[File:Vector model of orbital angular momentum.svg|250px|"250px"|right|thumb|Illustration of the vector model of orbital angular momentum.]] | |||
{{main|Vector model of the atom}} | |||
Since the angular momenta are quantum operators, they cannot be drawn as vectors like in classical mechanics. Nevertheless, it is common to depict them heuristically in this way. Depicted on the right is a set of states with quantum numbers <math>\ell=2</math>, and <math>m_\ell=-2,-1,0,1,2</math> for the five cones from bottom to top. Since <math>|L|=\sqrt{L^2}=\hbar \sqrt{6}</math>, the vectors are all shown with length <math>\hbar \sqrt{6}</math>. The rings represent the fact that <math>L_z</math> is known with certainty, but <math>L_x</math> and <math>L_y</math> are unknown; therefore every classical vector with the appropriate length and ''z''-component is drawn, forming a cone. The expected value of the angular momentum for a given ensemble of systems in the quantum state characterized by <math> \ell</math> and <math>m_\ell</math> could be somewhere on this cone while it cannot be defined for a single system (since the components of <math>L</math> do not commute with each other). | |||
< | |||
===Quantization in macroscopic systems=== | |||
The quantization rules are technically true even for macroscopic systems, like the angular momentum '''L''' of a spinning tire. However they have no observable effect. For example, if <math>L_z/\hbar</math> is roughly 100000000, it makes essentially no difference whether the precise value is an integer like 100000000 or 100000001, or a non-integer like 100000000.2—the discrete steps are too small to notice. | |||
==Angular momentum as the generator of rotations== | |||
{{see also|Total angular momentum quantum number}} | |||
The most general and fundamental definition of angular momentum is as the ''generator'' of rotations.<ref name=littlejohn>{{cite web|url=http://bohr.physics.berkeley.edu/classes/221/1011/notes/spinrot.pdf|title= Lecture notes on rotations in quantum mechanics|first= Robert |last=Littlejohn|accessdate= 13 Jan 2012|work=[http://bohr.physics.berkeley.edu/classes/221/1011/221.html Physics 221B Spring 2011]|year=2011}}</ref> More specifically, let <math>R(\hat{n},\phi)</math> be a [[Rotation operator (quantum mechanics)|rotation operator]], which rotates any quantum state about axis <math>\hat{n}</math> by angle <math>\phi</math>. As <math>\phi\rightarrow 0</math>, the operator <math>R(\hat{n},\phi)</math> approaches the [[identity operator]], because a rotation of 0° maps all states to themselves. Then the angular momentum operator <math>J_{\hat{n}}</math> about axis <math>\hat{n}</math> is defined as:<ref name=littlejohn/> | |||
:<math>J_{\hat{n}} \equiv i \hbar \lim_{\phi\rightarrow 0} \frac{R(\hat{n},\phi) - 1}{\phi}</math> | |||
where 1 is the [[identity operator]]. Remark also that ''R'' is an additive morphism : <math>R(\hat{n},\phi_1+\phi_2)=R(\hat{n},\phi_1)R(\hat{n},\phi_2)</math> ; as a consequence<ref name=littlejohn/> | |||
:<math>R(\hat{n},\phi) = \exp(-i \phi J_{\hat{n}}/\hbar)</math> | |||
where exp is [[matrix exponential]]. | |||
In simpler terms, the total angular momentum operator characterizes how a quantum system is changed when it is rotated. The relationship between angular momentum operators and rotation operators is the same as the relationship between [[Lie algebra]]s and [[Lie group]]s in mathematics, as discussed further below. | |||
[[File:RotationOperators.svg|thumb|300px|The different types of [[rotation operator (quantum mechanics)|rotation operators]]. <u>Top</u>: Two particles, with spin states indicated schematically by the arrows. <u>(A)</u> The operator ''R'', related to '''J''', rotates the entire system. <u>(B)</u> The operator ''R''<sub>spatial</sub>, related to '''L''', rotates the particle positions without altering their internal spin states. <u>(C)</u> The operator ''R''<sub>internal</sub>, related to '''S''', rotates the particles' internal spin states without changing their positions.]] | |||
Just as '''J''' is the generator for [[rotation operator (quantum mechanics)|rotation operators]], '''L''' and '''S''' are generators for modified partial rotation operators. The operator | |||
:<math>R_\mathrm{spatial}(\hat{n},\phi) = \exp(-i \phi L_{\hat{n}}/\hbar),</math> | |||
rotates the position (in space) of all particles and fields, without rotating the internal (spin) state of any particle. Likewise, the operator | |||
:<math>R_\mathrm{internal}(\hat{n},\phi) = \exp(-i \phi S_{\hat{n}}/\hbar),</math> | |||
rotates the internal (spin) state of all particles, without moving any particles or fields in space. The relation '''J'''='''L'''+'''S''' comes from: | |||
:<math>R(\hat{n},\phi) = R_\mathrm{internal}(\hat{n},\phi) R_\mathrm{spatial}(\hat{n},\phi)</math> | |||
i.e. if the positions are rotated, and then the internal states are rotated, then altogether the complete system has been rotated. | |||
===SU(2), SO(3), and 360° rotations=== | |||
{{main|Spin (physics)}} | |||
Although one might expect <math>R(\hat{n},360^\circ) = 1</math> (a rotation of 360° is the identity operator), this is ''not'' assumed in quantum mechanics, and it turns out it is often not true: When the total angular momentum quantum number is a half-integer (1/2, 3/2, etc.), <math>R(\hat{n},360^\circ) = -1</math>, and when it is an integer, <math>R(\hat{n},360^\circ) = +1</math>.<ref name=littlejohn/> Mathematically, the structure of rotations in the universe is ''not'' [[SO(3)]], the [[Lie group|group]] of three-dimensional rotations in classical mechanics. Instead, it is [[SU(2)]], which is identical to SO(3) for small rotations, but where a 360° rotation is mathematically distinguished from a rotation of 0°. (A rotation of 720° is, however, the same as a rotation of 0°.)<ref name=littlejohn/> | |||
\ | |||
< | |||
On the other hand, <math>R_\mathrm{spatial}(\hat{n},360^\circ) = +1</math> in all circumstances, because a 360° rotation of a ''spatial'' configuration is the same as no rotation at all. (This is different from a 360° rotation of the ''internal'' (spin) state of the particle, which might or might not be the same as no rotation at all.) In other words, the <math>R_\mathrm{spatial}</math> operators carry the structure of [[SO(3)]], while <math>R</math> and <math>R_\mathrm{internal}</math> carry the structure of [[SU(2)]]. | |||
From the equation <math>+1=R_\mathrm{spatial}(\hat{z},360^\circ) = \exp(-2\pi i L_z /\hbar)</math>, one picks an eigenstate <math> L_z |\psi\rangle = m\hbar |\psi\rangle</math> and draws | |||
:<math> e^{-2\pi i m} = 1 </math> | |||
which is to say that the orbital angular momentum quantum numbers can only be integers, not half-integers. | |||
===Connection to representation theory=== | |||
{{main|Particle physics and representation theory|Representation theory of SU(2)}} | |||
Starting with a certain quantum state <math>|\psi_0\rangle</math>, consider the set of states <math>R(\hat{n},\phi)|\psi_0\rangle</math> for all possible <math>\hat{n}</math> and <math>\phi</math>, i.e. the set of states that come about from rotating the starting state in every possible way. This is a [[vector space]], and therefore the manner in which the rotation operators map one state onto another is a [[group representation|''representation'']] of the group of rotation operators. | |||
:''When rotation operators act on quantum states, it forms a [[group representation|representation]] of the [[Lie group]] [[SU(2)]] (for R and R<sub>internal</sub>), or [[SO(3)]] (for R<sub>spatial</sub>).'' | |||
From the relation between '''J''' and rotation operators, | |||
:''When angular momentum operators act on quantum states, it forms a [[group representation|representation]] of the [[Lie algebra]] [[SU(2)]] or [[SO(3)]].'' | |||
(The Lie algebras of SU(2) and SO(3) are identical.) | |||
The ladder operator derivation above is a method for classifying the representations of the Lie algebra SU(2). | |||
===Connection to commutation relations=== | |||
Classical rotations do not commute with each other: For example, rotating 1° about the ''x''-axis then 1° about the ''y''-axis gives a slightly different overall rotation than rotating 1° about the ''y''-axis then 1° about the ''x''-axis. By carefully analyzing this noncommutativity, the commutation relations of the angular momentum operators can be derived.<ref name=littlejohn/> | |||
(This same calculational procedure is one way to answer the mathematical question "What is the [[Lie algebra]] of the [[Lie group]]s [[SO(3)]] or [[SU(2)]]?") | |||
==Conservation of angular momentum== | |||
The [[Hamiltonian (quantum mechanics)|Hamiltonian]] ''H'' represents the energy and dynamics of the system. In a spherically-symmetric situation, the Hamiltonian is invariant under rotations: | |||
:<math>RHR^{-1}=H</math> | |||
where ''R'' is a [[rotation operator (quantum mechanics)|rotation operator]]. As a consequence, <math>[H,R]=0</math>, and then <math>[H,\mathbf{J}]=0</math> due to the relationship between '''J''' and ''R''. By the [[Ehrenfest theorem]], it follows that '''J''' is conserved. | |||
To summarize, if ''H'' is rotationally-invariant (spherically symmetric), then total angular momentum '''J''' is conserved. This is an example of [[Noether's theorem]]. | |||
If ''H'' is just the Hamiltonian for one particle, the total angular momentum of that one particle is conserved when the particle is in a [[central potential]] (i.e., when the potential energy function depends only on <math>|\mathbf{r}|</math>). Alternatively, ''H'' may be the Hamiltonian of all particles and fields in the universe, and then ''H'' is ''always'' rotationally-invariant, as the fundamental laws of physics of the universe are the same regardless of orientation. This is the basis for saying [[conservation of angular momentum]] is a general principle of physics. | |||
For a particle without spin, '''J'''='''L''', so orbital angular momentum is conserved in the same circumstances. When the spin is nonzero, the [[spin-orbit interaction]] allows angular momentum to transfer from '''L''' to '''S''' or back. Therefore, '''L''' is not, on its own, conserved. | |||
==Angular momentum coupling== | |||
{{main|Angular momentum coupling|Clebsch–Gordan coefficients}} | |||
< | Often, two or more sorts of angular momentum interact with each other, so that angular momentum can transfer from one to the other. For example, in [[spin-orbit coupling]], angular momentum can transfer between '''L''' and '''S''', but only the total '''J'''='''L'''+'''S''' is conserved. In another example, in an atom with two electrons, each has its own angular momentum '''J'''<sub>1</sub> and '''J'''<sub>2</sub>, but only the total '''J'''='''J'''<sub>1</sub>+'''J'''<sub>2</sub> is conserved. | ||
< | |||
In these situations, it is often useful to know the relationship between, on the one hand, states where <math>(J_1)_z, (J_1)^2, (J_2)_z, (J_2)^2</math> all have definite values, and on the other hand, states where <math>(J_1)^2, (J_2)^2, J^2, J_z</math> all have definite values, as the latter four are usually conserved (constants of motion). The procedure to go back and forth between these [[basis (linear algebra)|bases]] is to use [[Clebsch–Gordan coefficients]]. | |||
One important result in this field is that a relationship between the quantum numbers for <math>(J_1)^2, (J_2)^2, J^2</math>: | |||
:<math> j \in \{ |j_1-j_2|, (|j_1-j_2|+1), \ldots, (j_1 + j_2) \} </math>. | |||
For an atom or molecule with '''J''' = '''L''' + '''S''', the [[term symbol]] gives the quantum numbers associated with the operators <math>L^2, S^2, J^2</math>. | |||
==Orbital angular momentum in spherical coordinates== | |||
Angular momentum operators usually occur when solving a problem with [[spherical symmetry]] in [[spherical coordinates]]. The angular momentum in space representation is | |||
<ref>{{Cite book | |||
| publisher = Springer Berlin Heidelberg | |||
| isbn = 978-3-540-46215-6 | |||
| title = Quantum Mechanics | |||
| location = Berlin, Heidelberg | |||
| accessdate = 2011-03-29 | |||
| year = 2007 | |||
| url = http://www.springerlink.com/index/10.1007/978-3-540-46216-3 | |||
| page= 70 | |||
}}</ref> | |||
<math> | : <math>L_{x}=i\hbar\left(\sin\phi\frac{\partial}{\partial\theta}+\cot\theta\cos\phi\frac{\partial}{\partial\phi}\right), </math> | ||
</math | |||
: <math>L_{y}=i\hbar\left(-\cos\phi\frac{\partial}{\partial\theta}+\cot\theta\sin\phi\frac{\partial}{\partial\phi}\right), </math> | |||
: <math>L_{z}=-i\hbar\frac{\partial}{\partial\phi,}</math> | |||
and | |||
<math> | : <math>L^2 = -\hbar^2 \left(\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\left( \sin\theta \frac{\partial}{\partial \theta}\right) + \frac{1}{\sin^2\theta}\frac{\partial^2}{\partial \phi^2}\right). </math> | ||
\ | |||
When solving to find [[eigenstate]]s of this operator, we obtain the following | |||
: <math> L^2 \mid l, m \rang = {\hbar}^2 l(l+1) | l, m \rang </math> | |||
: <math> L_z \mid l, m \rang = \hbar m | l, m \rang </math> | |||
where | |||
:<math> \lang \theta , \phi | l, m \rang = Y_{l,m}(\theta,\phi)</math> | |||
are the [[spherical harmonic]]s. | |||
<math>\ | |||
<math>\ | |||
<math>\ | |||
==See also== | ==See also== | ||
*[[ | *[[Runge–Lenz vector]] (used to describe the shape and orientation of bodies in orbit) | ||
*[[ | *[[Holstein–Primakoff transformation]] | ||
*[[Vector model of the atom]] | |||
*[[Pauli–Lubanski pseudovector]] | |||
*[[Angular momentum diagrams (quantum mechanics)]] | |||
*[[Spherical basis]] | |||
*[ | *[[Tensor operator]] | ||
*[[Orbital magnetization]] | |||
*[ | |||
*[ | |||
*[ | |||
*[ | |||
*[ | |||
==References== | ==References== | ||
<references/> | |||
== Further reading == | ==Further reading== | ||
* ''Quantum Mechanics Demystified'', D. McMahon, Mc Graw Hill (USA), 2006, ISBN(10-) 0-07-145546 9 | |||
* | * ''Quantum mechanics'', E. Zaarur, Y. Peleg, R. Pnini, Schaum’s Easy Oulines Crash Course, Mc Graw Hill (USA), 2006, ISBN (10-)007-145533-7 ISBN (13-)978-007-145533-6 | ||
* | * ''Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2nd Edition)'', R. Eisberg, R. Resnick, John Wiley & Sons, 1985, ISBN 978-0-471-87373-0 | ||
* | * ''Quantum Mechanics'', E. Abers, Pearson Ed., Addison Wesley, Prentice Hall Inc, 2004, ISBN 978-0-13-146100-0 | ||
* | * ''Physics of Atoms and Molecules'', B.H. Bransden, C.J.Joachain, Longman, 1983, ISBN 0-582-44401-2 | ||
* | |||
{{ | {{Physics operator}} | ||
[[ | [[Category:Rotational symmetry]] | ||
[[ | [[Category:Quantum mechanics]] | ||
Revision as of 23:06, 14 August 2014
In case you look at the checklist of the Forbes 40 richest folks in Singapore, you will notice many who made their fortunes growing and investing in real estate. Or simply look around you – the average Singaporean's wealth in all probability comes more from the appreciation of his HDB flat or non-public property than from another asset.
As my husband and I are also Singapore PR, we plan to take our criticism to our MP as properly, hopefully the government will turn into conscious of this drawback or perhaps they knew about it already, but it is time to take some action to right this lengthy standing grievance among patrons, and even amongst brokers who acquired shunned out from offers like my poor agent. She misplaced a sale for certain and unbeknownst to her, she in all probability never had an opportunity with that property proper from the start! I feel sorry for her, and appreciated her effort in alerting us about this unit and attempting to get us the property; but I'm a bit of aggravated or perhaps a bit resentful that we lost that condo basically as a result of we had been attached to her or any co-broke agent?
A very powerful part of the process of finding and securing housing is finding a superb estate agent, which is greatest achieved by word of mouth. As soon as expats have managed this feat, what follows is significantly less complicated and less annoying. Steps to renting property in Singapore We've got collected a cross-section of the most effective property resources and repair providers, multi function simple-to-use location, to additional streamline your property purchase or sale. Whether or not you are a first time home buyer or a seasoned seller, you will discover SingaporePropertyExchange.com the essential resource to strengthen your property transaction. iii) for such different period as the Registrar might enable, and had been resident in Singapore throughout that period. ECG Property Pte. Ltd.
Have passed an industry examination i.e Common Examination for House Agents (CEHA) or Actual Estate Company (REA) exam, or equal; Exclusive agents are extra willing to share listing data thus guaranteeing the widest doable coverage inside the actual property group thru Multiple Listings and Networking. Accepting a critical provide is easier since your agent is fully aware of all marketing exercise related together with your property. This reduces your having to verify with a number of agents for another affords. Price control is well achieved. Paint work in good restore-discuss along with your Property Advisor if main works are nonetheless to be accomplished. Softening in residential property costs continue, led by 2.eight per cent decline in the index for Remainder of Central Area
With the steam of an overheated property market dying down, the excitement has now shifted to builders playing discount video games to push new ec launch singapore [that guy] initiatives or clear outdated stock. With so many ‘great offers', patrons are spoiled for choices. In case you overprice your house, buyers shall be delay by the worth. Because of this your own home may take longer to sell, and end up being sold at a lower cost. Patrons may think that you are desperate in promoting (so that you have interaction multiple brokers to sell it off quick). Since they think you might be determined, they may not offer you a great value. Additionally, estate agents are responsibility-certain to avoid another potential conflicts of interest (equivalent to if a celebration to the transaction is related to the agent) until the client's waiver is obtained.
Like anywhere else, cash goes farther when you're exterior the prime districts. In case you plan to stay in a central location, you will have to settle for much less space or fewer onsite services. While rental prices are nonetheless high, 2013 has seen costs adjusting downwards in the higher brackets above $10,000 and the central districts flat-lining. Nevertheless, good value properties in the outer regions and decrease priced items have retained and even seen will increase as individuals typically have been downsizing
It's also usually free to tenants. However tenants paying lower than $three,500 monthly in rental typically pay a half month commission for annually of rental. For rentals above $3,500, tenants don't pay any commission. Does the acquisition process differ for residential, retail, office and industrial properties? Our Guide will assist you to have a head begin within the SEARCH ENGINE OPTIMIZATION bandwagon by performing the right WEBSITE POSITIONING implementation with our custom-made WEBSITE POSITIONING ranking tatics. Basic Search Engine Optimization Capacity to add / edit or delete Challenge Change Ordering of Venture Unpublish or Publish a Undertaking Capability to add / edit or delete a banner of the Undertaking I feel what amazes us firstly is that each owner and agent have to be there with us! Month-to-month rent is $3,888
In quantum mechanics, the angular momentum operator is one of several related operators analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry. In both classical and quantum mechanical systems, angular momentum (together with linear momentum and energy) is one of the three fundamental properties of motion.[1]
There are several angular momentum operators: total angular momentum (usually denoted J), orbital angular momentum (usually denoted L), and spin angular momentum (spin for short, usually denoted S). The term "angular momentum operator" can (confusingly) refer to either the total or the orbital angular momentum. Total angular momentum is always conserved, see Noether's theorem.
Spin, orbital, and total angular momentum
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

The classical definition of angular momentum is . This can be carried over to quantum mechanics, by reinterpreting r as the quantum position operator and p as the quantum momentum operator. L is then an operator, specifically called the orbital angular momentum operator. Specifically, L is a vector operator, meaning , where Lx, Ly, Lz are three different operators.
However, there is another type of angular momentum, called spin angular momentum (more often shortened to spin), represented by the spin operator S. Almost all elementary particles have spin. Spin is often depicted as a particle literally spinning around an axis, but this is a misleading and inaccurate picture: Spin is an intrinsic property of a particle, unrelated to any sort of motion in space. All elementary particles have a characteristic spin, for example electrons always have "spin 1/2" while photons always have "spin 1".
Finally, there is total angular momentum J, which combines both the spin and orbital angular momentum of a particle or system:
Conservation of angular momentum states that J for a closed system, or J for the whole universe, is conserved. However, L and S are not generally conserved. For example, the spin–orbit interaction allows angular momentum to transfer back and forth between L and S, with the total J remaining constant.
Orbital angular momentum operator
Orbital angular momentum L is mathematically defined as the cross product of a wave function's position operator (r) and momentum operator (p):
This is analogous to the definition of angular momentum in classical physics.
In the special case of a single particle with no electric charge and no spin, the angular momentum operator can be written in the position basis as a single vector equation:
where ∇ is the vector differential operator, del.
Commutation relations
Commutation relations between components
The orbital angular momentum operator is a vector operator, meaning it can be written in terms of its vector components . The components have the following commutation relations with each other:[2]
or in symbols,
where εlmn denotes the Levi-Civita symbol, and l,m,n are Cartesian coordinates (each can be x, y or z), and [, ] is the commutator
These can be proved as a direct consequence of the canonical commutation relations , where δlm is the Kronecker delta.
There is an analogous relationship to the commutator in classical physics which is central to the theory of canonical transformations of Hamilton's equations of motion:[3]
(summation over generalized coordinate index i implied) where, in this bilinear expression, is the Poisson bracket of two functions with respect to the canonical (generalized) coordinates . "... identification of the canonical angular momentum as the generator of rigid rotation of [a system of particles] leads to a number of interesting and important Poisson bracket relations."[4] Among these are:
Here, , for example, is a transformation generated by the generalized momentum conjugate to :
It can be shown[5] (using Cartesian coordinates x, y and z for each particle i in the system) that
This generating function has the physical significance of being the z-component of the total angular momentum:
It is important to recognize that the Poisson bracket is an analogue, not the commutator in disguise. Hamilton's equations do not generalize to quantum mechanics because they assume that the position and momentum of a particle can be known simultaneously to infinite precision at any point in time. See the section "Generalization to quantum mechanics through Poisson bracket" in the article on Hamiltonian mechanics for details and additional references.
The same commutation relations apply for the other angular momentum operators (spin and total angular momentum):[6]
These can be assumed to hold in analogy with L. Alternatively, they can be derived as discussed below.
These commutation relations mean that L has the mathematical structure of a Lie algebra. In this case, the Lie algebra is SU(2) or SO(3), the rotation group in three dimensions. The same is true of J and S. The reason is discussed below.
These commutation relations are relevant for measurement and uncertainty, as discussed further below.
Commutation relations involving vector magnitude
Like any vector, a magnitude can be defined for the orbital angular momentum operator,
L2 is another quantum operator. It commutes with the components of L,
One way to prove that these operators commute is to start from the [Lℓ, Lm] commutation relations in the previous section:
Click [show] on the right to see a proof of [L2, Lx] = 0, starting from the [Lℓ, Lm] commutation relations[7]
Mathematically, L2 is a Casimir invariant of the Lie algebra SO(3) spanned by L.
In the classical case, L is the orbital angular momentum of the entire system of particles, n is the unit vector along one of the Cartesian axes and we also have Poisson pseudo-commutation of L with each of its Cartesian components:[8]
with selecting one of the Cartesian components of .
The same commutation relations apply for the other angular momentum operators (spin and total angular momentum):
Uncertainty principle
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. In general, in quantum mechanics, when two observable operators do not commute, they are called incompatible observables. Two incompatible observables cannot be measured simultaneously; instead they satisfy an uncertainty principle. The more accurately one observable is known, the less accurately the other one can be known. Just as there is an uncertainty principle relating position and momentum, there are uncertainty principles for angular momentum.
The Robertson–Schrödinger relation gives the following uncertainty principle:
where is the standard deviation in the measured values of X and denotes the expectation value of X. This inequality is also true if x,y,z are rearranged, or if L is replaced by J or S.
Therefore, two orthogonal components of angular momentum cannot be simultaneously known or measured, except in special cases such as .
It is, however, possible to simultaneously measure or specify L2 and any one component of L; for example, L2 and Lz. This is often useful, and the values are characterized by azimuthal quantum number and magnetic quantum number, as discussed further below.
Quantization
DTZ's public sale group in Singapore auctions all forms of residential, workplace and retail properties, outlets, homes, lodges, boarding homes, industrial buildings and development websites. Auctions are at present held as soon as a month.
We will not only get you a property at a rock-backside price but also in an space that you've got longed for. You simply must chill out back after giving us the accountability. We will assure you 100% satisfaction. Since we now have been working in the Singapore actual property market for a very long time, we know the place you may get the best property at the right price. You will also be extremely benefited by choosing us, as we may even let you know about the precise time to invest in the Singapore actual property market.
The Hexacube is offering new ec launch singapore business property for sale Singapore investors want to contemplate. Residents of the realm will likely appreciate that they'll customize the business area that they wish to purchase as properly. This venture represents one of the crucial expansive buildings offered in Singapore up to now. Many investors will possible want to try how they will customise the property that they do determine to buy by means of here. This location has offered folks the prospect that they should understand extra about how this course of can work as well.
Singapore has been beckoning to traders ever since the value of properties in Singapore started sky rocketing just a few years again. Many businesses have their places of work in Singapore and prefer to own their own workplace area within the country once they decide to have a everlasting office. Rentals in Singapore in the corporate sector can make sense for some time until a business has discovered a agency footing. Finding Commercial Property Singapore takes a variety of time and effort but might be very rewarding in the long term.
is changing into a rising pattern among Singaporeans as the standard of living is increasing over time and more Singaporeans have abundance of capital to invest on properties. Investing in the personal properties in Singapore I would like to applaud you for arising with such a book which covers the secrets and techniques and tips of among the profitable Singapore property buyers. I believe many novice investors will profit quite a bit from studying and making use of some of the tips shared by the gurus." – Woo Chee Hoe Special bonus for consumers of Secrets of Singapore Property Gurus Actually, I can't consider one other resource on the market that teaches you all the points above about Singapore property at such a low value. Can you? Condominium For Sale (D09) – Yong An Park For Lease
In 12 months 2013, c ommercial retails, shoebox residences and mass market properties continued to be the celebrities of the property market. Models are snapped up in report time and at document breaking prices. Builders are having fun with overwhelming demand and patrons need more. We feel that these segments of the property market are booming is a repercussion of the property cooling measures no.6 and no. 7. With additional buyer's stamp responsibility imposed on residential properties, buyers change their focus to commercial and industrial properties. I imagine every property purchasers need their property funding to understand in value.
In quantum mechanics, angular momentum is quantized – that is, it cannot vary continuously, but only in "quantum leaps" between certain allowed values. For any system, the following restrictions on measurement results apply, where is reduced Planck constant:
| If you measure... | ...the result can be... | Notes |
|---|---|---|
| Lz | , where | m is sometimes called "magnetic quantum number". This same quantization rule holds for any component of L, e.g. Lx or Ly. This rule is sometimes called spatial quantization.[9] |
| Sz or Jz | , where | For Sz, m is sometimes called "spin projection quantum number". For Jz, m is sometimes called "total angular momentum projection quantum number". This same quantization rule holds for any component of S or J, e.g. Sx or Jy. |
| , where | L2 is defined by . is sometimes called "azimuthal quantum number" or "orbital quantum number". | |
| , where | s is called spin quantum number or just "spin". For example, a spin-½ particle is a particle where s=½. | |
| , where | j is sometimes called "total angular momentum quantum number". | |
| and simultaneously |
for , and for where and |
(See above for terminology.) |
| and simultaneously |
for , and for where and |
(See above for terminology.) |
| and simultaneously |
for , and for where and |
(See above for terminology.) |

Derivation using ladder operators
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. A common way to derive the quantization rules above is the method of ladder operators.[10] The ladder operators are defined:
Suppose a state is a state in the simultaneous eigenbasis of and (i.e., a state with a single, definite value of and a single, definite value of ). Then using the commutation relations, one can prove that and are also in the simultaneous eigenbasis, with the same value of , but where is increased or decreased by , respectively. (It is also possible that one or both of these vectors is the zero vector.) (For a proof, see ladder operator#angular momentum.)
By manipulating these ladder operators and using the commutation rules, it is possible to prove almost all of the quantization rules above.
| Click [show] on the right to see more details in the ladder-operator proof of the quantization rules[10] |
|---|
| Before starting the main proof, we will note a useful fact: That are positive-semidefinite operators, meaning that all their eigenvalues are nonnegative. That also implies that the same is true for their sums, including and . The reason is because the square of any Hermitian operator is always positive semidefinite. (A Hermitian operator has real eigenvalues, so the squares of those eigenvalues are nonnegative.)
As above, assume that a state is a state in the simultaneous eigenbasis of and . Its eigenvalue with respect to can be written in the form for some real number j > 0 (because as mentioned in the previous paragraph, has nonnegative eigenvalues), and its eigenvalue with respect to can be written for some real number m. Instead of we will use the more descriptive notation . Next, consider the sequence ("ladder") of states Some entries in this infinite sequence may be the zero vector (as we will see). However, as described above, all the nonzero entries have the same value of , and among the nonzero entries, each entry has a value of which is exactly more than the previous entry. In this ladder, there can only be a finite number of nonzero entries, with infinite copies of the zero vector on the left and right. The reason is, as mentioned above, is positive-semidefinite, so if any quantum state is an eigenvector of both and , the former eigenvalue is larger. The states in the ladder all have the same eigenvalue, but going very far to the left or the right, the eigenvalue gets larger and larger. The only possible resolution is, as mentioned, that there are only finitely many nonzero entries in the ladder. Now, consider the last nonzero entry to the right of the ladder, . This state has the property that . As proven in the ladder operator article, If this is zero, then , so or . However, because is positive-semidefinite, , which means that the only possibility is . Similarly, consider the first nonzero entry on the left of the ladder, . This state has the property that . As proven in the ladder operator article, As above, the only possibility is that Since m changes by 1 on each step of the ladder, is an integer, so j is an integer or half-integer (0 or 0.5 or 1 or 1.5...). |
Since S and L have the same commutation relations as J, the same ladder analysis works for them.
The ladder-operator analysis does not explain one aspect of the quantization rules above: the fact that L (unlike J and S) cannot have half-integer quantum numbers. This fact can be proven (at least in the special case of one particle) by writing down every possible eigenfunction of L2 and Lz, (they are the spherical harmonics), and seeing explicitly that none of them have half-integer quantum numbers.[11] An alternative derivation is below.
Visual interpretation
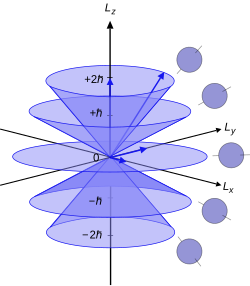
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. Since the angular momenta are quantum operators, they cannot be drawn as vectors like in classical mechanics. Nevertheless, it is common to depict them heuristically in this way. Depicted on the right is a set of states with quantum numbers , and for the five cones from bottom to top. Since , the vectors are all shown with length . The rings represent the fact that is known with certainty, but and are unknown; therefore every classical vector with the appropriate length and z-component is drawn, forming a cone. The expected value of the angular momentum for a given ensemble of systems in the quantum state characterized by and could be somewhere on this cone while it cannot be defined for a single system (since the components of do not commute with each other).
Quantization in macroscopic systems
The quantization rules are technically true even for macroscopic systems, like the angular momentum L of a spinning tire. However they have no observable effect. For example, if is roughly 100000000, it makes essentially no difference whether the precise value is an integer like 100000000 or 100000001, or a non-integer like 100000000.2—the discrete steps are too small to notice.
Angular momentum as the generator of rotations
DTZ's public sale group in Singapore auctions all forms of residential, workplace and retail properties, outlets, homes, lodges, boarding homes, industrial buildings and development websites. Auctions are at present held as soon as a month.
We will not only get you a property at a rock-backside price but also in an space that you've got longed for. You simply must chill out back after giving us the accountability. We will assure you 100% satisfaction. Since we now have been working in the Singapore actual property market for a very long time, we know the place you may get the best property at the right price. You will also be extremely benefited by choosing us, as we may even let you know about the precise time to invest in the Singapore actual property market.
The Hexacube is offering new ec launch singapore business property for sale Singapore investors want to contemplate. Residents of the realm will likely appreciate that they'll customize the business area that they wish to purchase as properly. This venture represents one of the crucial expansive buildings offered in Singapore up to now. Many investors will possible want to try how they will customise the property that they do determine to buy by means of here. This location has offered folks the prospect that they should understand extra about how this course of can work as well.
Singapore has been beckoning to traders ever since the value of properties in Singapore started sky rocketing just a few years again. Many businesses have their places of work in Singapore and prefer to own their own workplace area within the country once they decide to have a everlasting office. Rentals in Singapore in the corporate sector can make sense for some time until a business has discovered a agency footing. Finding Commercial Property Singapore takes a variety of time and effort but might be very rewarding in the long term.
is changing into a rising pattern among Singaporeans as the standard of living is increasing over time and more Singaporeans have abundance of capital to invest on properties. Investing in the personal properties in Singapore I would like to applaud you for arising with such a book which covers the secrets and techniques and tips of among the profitable Singapore property buyers. I believe many novice investors will profit quite a bit from studying and making use of some of the tips shared by the gurus." – Woo Chee Hoe Special bonus for consumers of Secrets of Singapore Property Gurus Actually, I can't consider one other resource on the market that teaches you all the points above about Singapore property at such a low value. Can you? Condominium For Sale (D09) – Yong An Park For Lease
In 12 months 2013, c ommercial retails, shoebox residences and mass market properties continued to be the celebrities of the property market. Models are snapped up in report time and at document breaking prices. Builders are having fun with overwhelming demand and patrons need more. We feel that these segments of the property market are booming is a repercussion of the property cooling measures no.6 and no. 7. With additional buyer's stamp responsibility imposed on residential properties, buyers change their focus to commercial and industrial properties. I imagine every property purchasers need their property funding to understand in value.
The most general and fundamental definition of angular momentum is as the generator of rotations.[6] More specifically, let be a rotation operator, which rotates any quantum state about axis by angle . As , the operator approaches the identity operator, because a rotation of 0° maps all states to themselves. Then the angular momentum operator about axis is defined as:[6]
where 1 is the identity operator. Remark also that R is an additive morphism : ; as a consequence[6]
where exp is matrix exponential.
In simpler terms, the total angular momentum operator characterizes how a quantum system is changed when it is rotated. The relationship between angular momentum operators and rotation operators is the same as the relationship between Lie algebras and Lie groups in mathematics, as discussed further below.

Just as J is the generator for rotation operators, L and S are generators for modified partial rotation operators. The operator
rotates the position (in space) of all particles and fields, without rotating the internal (spin) state of any particle. Likewise, the operator
rotates the internal (spin) state of all particles, without moving any particles or fields in space. The relation J=L+S comes from:
i.e. if the positions are rotated, and then the internal states are rotated, then altogether the complete system has been rotated.
SU(2), SO(3), and 360° rotations
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. Although one might expect (a rotation of 360° is the identity operator), this is not assumed in quantum mechanics, and it turns out it is often not true: When the total angular momentum quantum number is a half-integer (1/2, 3/2, etc.), , and when it is an integer, .[6] Mathematically, the structure of rotations in the universe is not SO(3), the group of three-dimensional rotations in classical mechanics. Instead, it is SU(2), which is identical to SO(3) for small rotations, but where a 360° rotation is mathematically distinguished from a rotation of 0°. (A rotation of 720° is, however, the same as a rotation of 0°.)[6]
On the other hand, in all circumstances, because a 360° rotation of a spatial configuration is the same as no rotation at all. (This is different from a 360° rotation of the internal (spin) state of the particle, which might or might not be the same as no rotation at all.) In other words, the operators carry the structure of SO(3), while and carry the structure of SU(2).
From the equation , one picks an eigenstate and draws
which is to say that the orbital angular momentum quantum numbers can only be integers, not half-integers.
Connection to representation theory
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. Starting with a certain quantum state , consider the set of states for all possible and , i.e. the set of states that come about from rotating the starting state in every possible way. This is a vector space, and therefore the manner in which the rotation operators map one state onto another is a representation of the group of rotation operators.
- When rotation operators act on quantum states, it forms a representation of the Lie group SU(2) (for R and Rinternal), or SO(3) (for Rspatial).
From the relation between J and rotation operators,
- When angular momentum operators act on quantum states, it forms a representation of the Lie algebra SU(2) or SO(3).
(The Lie algebras of SU(2) and SO(3) are identical.)
The ladder operator derivation above is a method for classifying the representations of the Lie algebra SU(2).
Connection to commutation relations
Classical rotations do not commute with each other: For example, rotating 1° about the x-axis then 1° about the y-axis gives a slightly different overall rotation than rotating 1° about the y-axis then 1° about the x-axis. By carefully analyzing this noncommutativity, the commutation relations of the angular momentum operators can be derived.[6]
(This same calculational procedure is one way to answer the mathematical question "What is the Lie algebra of the Lie groups SO(3) or SU(2)?")
Conservation of angular momentum
The Hamiltonian H represents the energy and dynamics of the system. In a spherically-symmetric situation, the Hamiltonian is invariant under rotations:
where R is a rotation operator. As a consequence, , and then due to the relationship between J and R. By the Ehrenfest theorem, it follows that J is conserved.
To summarize, if H is rotationally-invariant (spherically symmetric), then total angular momentum J is conserved. This is an example of Noether's theorem.
If H is just the Hamiltonian for one particle, the total angular momentum of that one particle is conserved when the particle is in a central potential (i.e., when the potential energy function depends only on ). Alternatively, H may be the Hamiltonian of all particles and fields in the universe, and then H is always rotationally-invariant, as the fundamental laws of physics of the universe are the same regardless of orientation. This is the basis for saying conservation of angular momentum is a general principle of physics.
For a particle without spin, J=L, so orbital angular momentum is conserved in the same circumstances. When the spin is nonzero, the spin-orbit interaction allows angular momentum to transfer from L to S or back. Therefore, L is not, on its own, conserved.
Angular momentum coupling
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
Often, two or more sorts of angular momentum interact with each other, so that angular momentum can transfer from one to the other. For example, in spin-orbit coupling, angular momentum can transfer between L and S, but only the total J=L+S is conserved. In another example, in an atom with two electrons, each has its own angular momentum J1 and J2, but only the total J=J1+J2 is conserved.
In these situations, it is often useful to know the relationship between, on the one hand, states where all have definite values, and on the other hand, states where all have definite values, as the latter four are usually conserved (constants of motion). The procedure to go back and forth between these bases is to use Clebsch–Gordan coefficients.
One important result in this field is that a relationship between the quantum numbers for :
For an atom or molecule with J = L + S, the term symbol gives the quantum numbers associated with the operators .
Orbital angular momentum in spherical coordinates
Angular momentum operators usually occur when solving a problem with spherical symmetry in spherical coordinates. The angular momentum in space representation is [12]
and
When solving to find eigenstates of this operator, we obtain the following
where
are the spherical harmonics.
See also
- Runge–Lenz vector (used to describe the shape and orientation of bodies in orbit)
- Holstein–Primakoff transformation
- Vector model of the atom
- Pauli–Lubanski pseudovector
- Angular momentum diagrams (quantum mechanics)
- Spherical basis
- Tensor operator
- Orbital magnetization
References
- ↑ Introductory Quantum Mechanics, Richard L. Liboff, 2nd Edition, ISBN 0-201-54715-5
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ H. Goldstein, C. P. Poole and J. Safko, Classical Mechanics, 3rd Edition, Addison-Wesley 2002, pp. 388 ff.
- ↑ Idem, pp. 408-411.
- ↑ Idem, p. 404.
- ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 Template:Cite web
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ Goldstein et al, p. 410
- ↑ Introduction to quantum mechanics: with applications to chemistry, by Linus Pauling, Edgar Bright Wilson, page 45, google books link
- ↑ 10.0 10.1 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
Further reading
- Quantum Mechanics Demystified, D. McMahon, Mc Graw Hill (USA), 2006, ISBN(10-) 0-07-145546 9
- Quantum mechanics, E. Zaarur, Y. Peleg, R. Pnini, Schaum’s Easy Oulines Crash Course, Mc Graw Hill (USA), 2006, ISBN (10-)007-145533-7 ISBN (13-)978-007-145533-6
- Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2nd Edition), R. Eisberg, R. Resnick, John Wiley & Sons, 1985, ISBN 978-0-471-87373-0
- Quantum Mechanics, E. Abers, Pearson Ed., Addison Wesley, Prentice Hall Inc, 2004, ISBN 978-0-13-146100-0
- Physics of Atoms and Molecules, B.H. Bransden, C.J.Joachain, Longman, 1983, ISBN 0-582-44401-2
What is directory submission? How does it help in the web site promotion? Several think directory submission is comparable to the information entry jobs and they assume it to be very simple and effortless. Sites like yahoo, Google etc have large net directories equivalent to the telephone directory we use. These directories are shop homes of relevant data about company issues and net sites all more than the planet. Hence for advertising a web website its details are submitted to the directory in exchange for a little fee.
Once more this directory submission can either be accomplished manually or implemented by way of automated services. When someone submits his internet site to a directory human editors have to go through them to verify top quality and other guidelines. With millions of internet internet sites coming in daily it is not effortless or it is quite stressful to go through them and verify for quality. So automated directory submissions was invented to examine for the submission recommendations. The advantage of this automated submission is that it is easy and less time consuming. It automatically checks and submits without delay.
But what really matters is regardless of whether the web directories can accept automated directory submission as they are very strict about the recommendations. Moreover if the category to which the submission is made is not selected effectively then it loses its purpose. You can not anticipate an automotive service to analyze which category your submission is finest suited dont you? Therefore even though the time factor favors automated directory submission it nonetheless has a lengthy way to go to outbid manual solutions.
Any item or service hitting the public market place needs to be advertised. Visit linkliciousdiscussionsldd - StreetFire Member in US to read why to see about it. There are several methods and means by means of which this advertisement can reach the general public. The print media, roadside banners, brochures, graphic boards and so on are some of the familiar advertising and marketing tactics followed. Be taught more on this related URL by visiting linklicious discount. Designed a professional web site to promote the business is the new and trendy marketing and advertising tool undertaken today to expose a business. For another standpoint, please consider checking out: is linklicious safe. Crucial characteristics like the Search engine marketing, SEM, directory submission, link developing and so on support to improve the search outcome when somebody searches in the search engine.
The net internet site payout along with the catchy content material and tags should be competent to bring in buyer visitors. And to enable this numerous factors are concerned crucial like the Search engine optimisation, SEM, directory submission, link creating and so on. any organization concern which requires off as a fresher should give away a press release and do the On-line Directories and Search Engine Submissions. Press Release is nothing at all but a public relation announcement about the new organization prospects. The details provided should be one hundred% original and no false or exaggerated content ought to be focused on. This is the principal door which opens up to the public who will trust what they see or read from this press release. This can also be completed during a course of a company when they roll out a new product or have introduced or opened a new retailer..
When you have any concerns about in which and how to utilize health answers, it is possible to e-mail us from the web page.




![[L_{x},L_{y}]=i\hbar L_{z},\;\;[L_{y},L_{z}]=i\hbar L_{x},\;\;[L_{z},L_{x}]=i\hbar L_{y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99fd42253a8dedf081a0cd1b6fbac2427b632d94)
![[L_{l},L_{m}]=i\hbar \varepsilon _{{lmn}}L_{n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b457b36b59588ebeb0c9b8c120de9d62df92b397)
![[X,Y]\equiv XY-YX](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c84058c92ea5997228b900a608540d8056f408c)
![{\displaystyle [x_{l},p_{m}]=i\hbar \delta _{lm}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2363420037b45b6869e104533de2bcb5720054da)
![{\displaystyle [u,v]_{q,p}={\frac {\partial u}{\partial q_{i}}}{\frac {\partial v}{\partial p_{i}}}-{\frac {\partial u}{\partial p_{i}}}{\frac {\partial v}{\partial q_{i}}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce4161f4c7ade8e60877ac4314c43c3021e52f4f)
![{\displaystyle [u,v]_{q,p}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54670499d86e6e133ce52c6693155b3fc2173a03)


![{\displaystyle [L_{l},L_{m}]=\varepsilon _{lmn}L_{n}.\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1a19d035b90c3f646c8557b7e6ef3e95e0fce7e)





![{\displaystyle [S_{l},S_{m}]=i\hbar \sum _{n=1}^{3}\varepsilon _{lmn}S_{n},\quad [J_{l},J_{m}]=i\hbar \sum _{n=1}^{3}\varepsilon _{lmn}J_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3d17b11ddf5ed2f1571fc23753f49c6e0911ca4)

![{\displaystyle [L^{2},L_{x}]=[L^{2},L_{y}]=[L^{2},L_{z}]=0~.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42a0b716b22801c94abe597ae9bf3891a541c589)
![[L^{2},L_{x}]=(L_{x}^{2}+L_{y}^{2}+L_{z}^{2})L_{x}-L_{x}(L_{x}^{2}+L_{y}^{2}+L_{z}^{2})](https://wikimedia.org/api/rest_v1/media/math/render/svg/13448f3ce0417eadadec61bdf7b7664fa367a190)

![{\displaystyle =L_{y}[L_{y},L_{x}]+[L_{y},L_{x}]L_{y}+L_{z}[L_{z},L_{x}]+[L_{z},L_{x}]L_{z}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cfb2eb2b018359ccacb60046038746a6ab02f42)


![[{\mathbf L}\cdot {\mathbf L},{\mathbf L}\cdot {\mathbf n}]=[L^{2},{\mathbf L}\cdot {\mathbf n}]=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/122fca1f5f97fbc904e26c3607ee3778f12b7539)


![[S^{2},S_{i}]=0,\quad [J^{2},J_{i}]=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/94bd503f094e93ce28e18d0c399b6050885efa61)























































































![{\displaystyle [H,R]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55ca790f49501a692d19581c1e02757584a8a859)
![[H,{\mathbf {J}}]=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/e603743252fac64718453f0a2e9685102a87c0f8)












